DENengin · Дисциплины

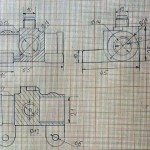
Разрезы заданных деталей (наклонный, ломаный, ступенчатый)

Задание:

1) перечертить данные неразъемные соединения соединение деталей

- Построить три проекции линии взаимного пересечения поверхностей заданных тел.

- Изобразить пересекающиеся поверхности и их линии пересечения в одном из видов аксонометрии.

- Построить три проекции линии взаимного пересечения поверхностей заданных тел.
- Изобразить пересекающиеся поверхности и их линии пересечения в одном из видов аксонометрии.

Задание:
1) построить две проекции линии пересечения поверхностей заданных тел (цилиндры и конусы) плоскостью;
2) определить видимость фигур сечения и поверхностей;
3) построить развертки боковых поверхностей тел.

Очень часто возникает вопрос, на какой из плоскостей проекции необходимо найти натуральную длину отрезка. Ответ: достаточно найти ее на ЛЮБОЙ из плоскостей проекции. Для доказательства данных слов, можно посмотреть вырезки из текстов печатных изданий различных авторов. (см. рис.1 и 2).

Задание:
1) построить две проекции линии пересечения поверхностей заданных тел (3-х, 4-х, 5-ти и 6-ти угольных призм и пирамид) плоскостью;
2) определить видимость фигур сечения и поверхностей;
3) построить развертки боковых поверхностей тел.

Когда нам нужно провести несколько линий параллельных друг другу здесь нам значительно упростит задачу рейсшина.

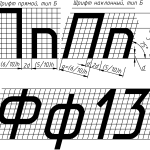
     Кратко, в табличном виде, представлены основные параметры букв, такие как:
    - высота букв;
    - ширина прописных букв;
    - ширина строчных букв;
    - толщина линий шрифта;
    - расстояние между буквами.

Скачать шрифты чертежные по ГОСТ 2.304-81 ЕСКД для AutoCAD, Word и других программ.
- ГОСТ тип А;
- ГОСТ тип Б;
- Символы ГОСТ тип А;
- Символы ГОСТ тип Б.
Файлы форматов: fon, ttf.

     Оглавление:

    1. Термины и определения
    2. Типы и размеры шрифта
    3. Русский алфавит (кириллица)
    4. Латинский алфавит
    5. Греческий алфавит
    6. Арабские и римские цифры
    7. Знаки
    8. Правила написания дробей, показателей, индексов и предельных отклонений

  В пространстве прямая общего положения в отличие от прямых частного положения проецируется на все плоскости проекций с искажением. Другими словами если отрезок параллелен плоскости, то он проецируется на неё без искажений.
       Поэтому при решении многих задач возникает необходимость по заданным проекциям отрезка определить его действительную величину. В таких случаях применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Содержит вопросы вида:
- принадлежности прямой плоскости;
- прямая, как линия наибольшего ската;
- прямая параллельная плоскости;
- параллельность пары плоскостей;
- пересечение прямой с плоскостью в точке;
- прямая, как горизонталь или фронталь плоскости.

ЗАДАНИЕ: через вершину В, треугольника ABC, провести плоскость, перпендикулярную стороне АС. Построить линию пересечения плоскостей. Определить видимость построенных плоскостей.

ЗАДАНИЕ: Построить плоскость, параллельную плоскости треугольника ABC и отстоящую от нее на какое-либо расстояние.

ЗАДАНИЕ: Определить расстояние от точки D до плоскости треугольника АВС и построить точку, симметричную точке D относительно данной плоскости.

Задание. Даны координаты точек A, B, C, D (табл. №1). Требуется решить в ортогональных проекциях следующие задачи:

1. Определить расстояние от точки D до плоскости треугольника АВС и построить точку, симметричную точке D относительно данной плоскости;
2. Построить плоскость, параллельная плоскости треугольника ABС и отстоящую от нее на 20 мм (30 мм или 40 мм);
3. Через вершину В треугольника ABC провести плоскость, перпендикулярную стороне АС. Построить линию пересечения плоскостей и определить их видимость.