Построить плоскость через вершину В, треугольника ABC, перпендикулярную стороне АС (пример выполнения)

Рис.1

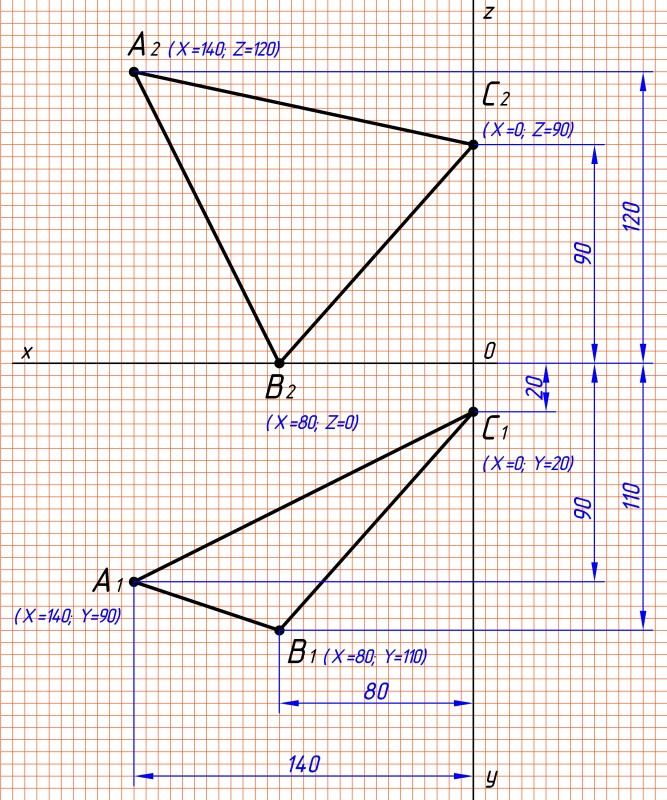
Строим плоскость треугольника АВС по заданным координатам варианта №17.

Данное задание обычно делается в масштабе 2 : 1 (см. рис.1):

Координаты по заданию:
A (70, 45, 60),
B (40, 55, 0),
C (0, 10, 45).

Если требуется в масштабе 2 : 1, то увеличиваем каждую координату на 2.
A (140, 90, 120),
B (80, 110, 0),
C (0, 20, 90).

Построить свой треугольник онлайн можно перейдя по ссылке.

Рис.2

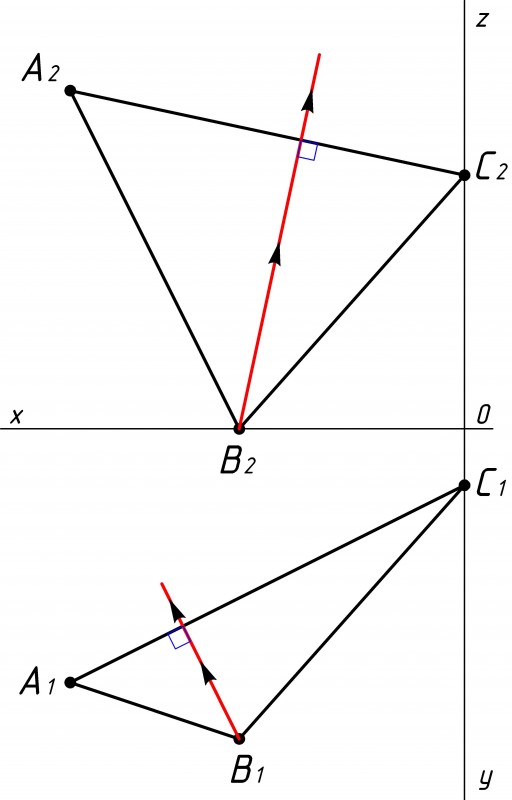
Для начала проведем из точки В, вершины треугольника АВС линию, перпендикулярную стороне АС (см. рис.2).

А именно, из точки В₁ проводим перпендикуляр к стороне А₁С₁, а из точки В₂ проводим перпендикуляр к стороне А₂С₂.

Рис.3

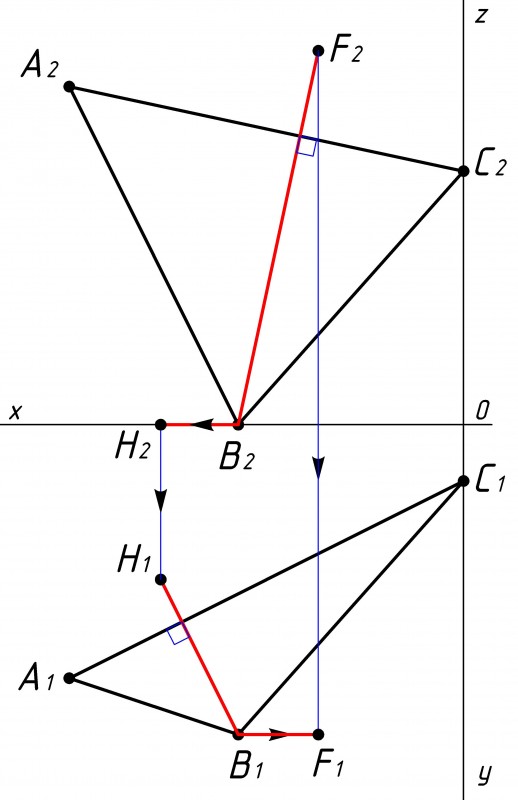
Затем проведем через точку В фронталь и горизонталь, чтобы использовать теорему о проекциях перпендикуляра к плоскости (см. рис.3).

Фронталь - линия, которая параллельна оси ОХ на горизонтальной плоскости проекции (нижняя часть),
Горизонталь - линия, которая параллельна оси ОХ на фронтальной плоскости проекции (верхняя часть).

Фронталь и горизонталь проводим в сторону проведения перпендикуляра на противоположной плоскости.
Т.е. фронталь через точку В₁ строим вправо, в сторону проведения перпендикуляра из точки В₂, а горизонталь через точку В₂ строим влево, в сторону проведения перпендикуляра из точки В₁.

Ограничиваем фронталь точкой F₁ и проецируем ее на фронтальной проекции перпендикуляра (точка F₂).
Ограничиваем горизонталь точкой Н₂ и проецируем ее на горизонтальной проекции перпендикуляра (точка Н₁).

Рис.4

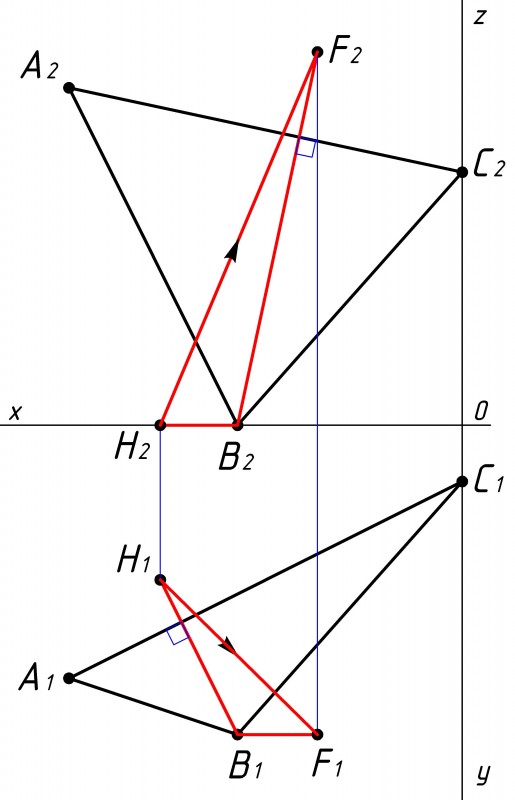
Достраиваем с помощью полученных точек плоскость треугольника ВFH (см. рис.4).

Для этого соединим точку В₁ с F₁, а точку В₂ с F₂.

Рис.5

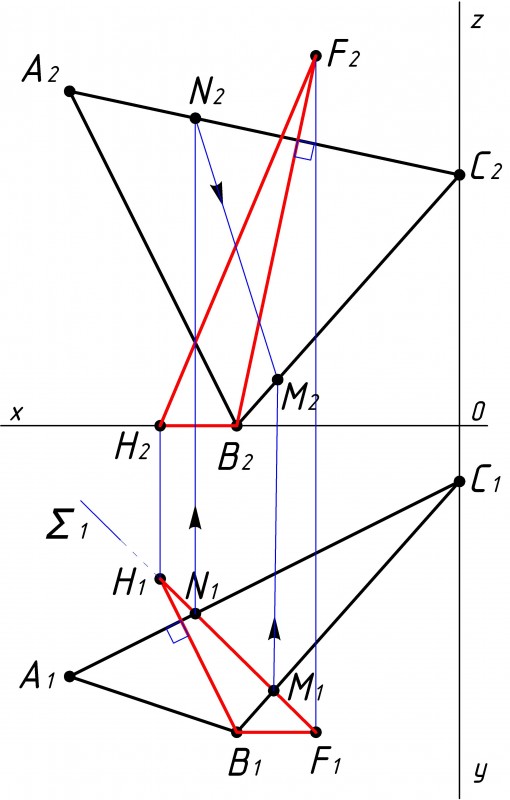
Теперь необходимо найти линию пересечения построенной плоскости треугольника ВFH с плоскостью треугольника ABC (см. рис.5).

Линия пересечения плоскостей определяется двумя общими точками. Одна общая точка у них уже есть – вершина B. Для определения второй общей точки находим точку пересечения стороны FH искомой плоскости с треугольником ABC.

Т.е. решаем задачу на пересечение прямой с плоскостью общего положения, для этого воспользуется вспомогательной плоскостью ∑, проведенной через FH.

Вспомогательную плоскостью ∑, можно провести через любую проекцию стороны FH.
В нашем примере мы начали строить на горизонтальной плоскости проекции. Поэтому вспомогательную плоскость ∑₁ проводим через H₁F₁ (горизонтальная проекция стороны FH).

Примечание: необязательно рисовать вспомогательную плоскость частного положения ∑₁, ее можно просто представить, что мы ее там проводим.

Находим две точки пересечения с треугольником ABC, точки N₁ и M₁. Проецируем их на фронтальную плоскость треугольника ABC и соединяем.

Рис.6

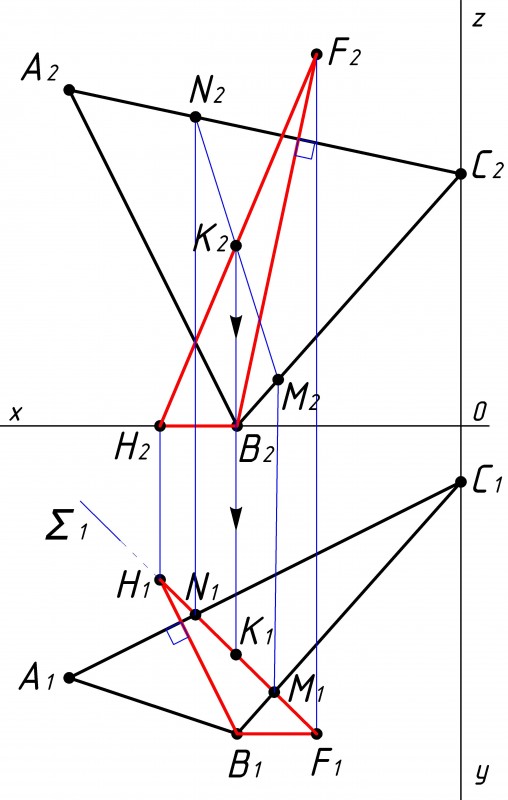
Получив линию N₂M₂, определяем точку пересечения со стороной FH и ставим точку К₂. Проецируем полученную точку на горизонтальную плоскость проекции на сторону FH и ставим точку К₁ (см. рис.6).

Рис.7

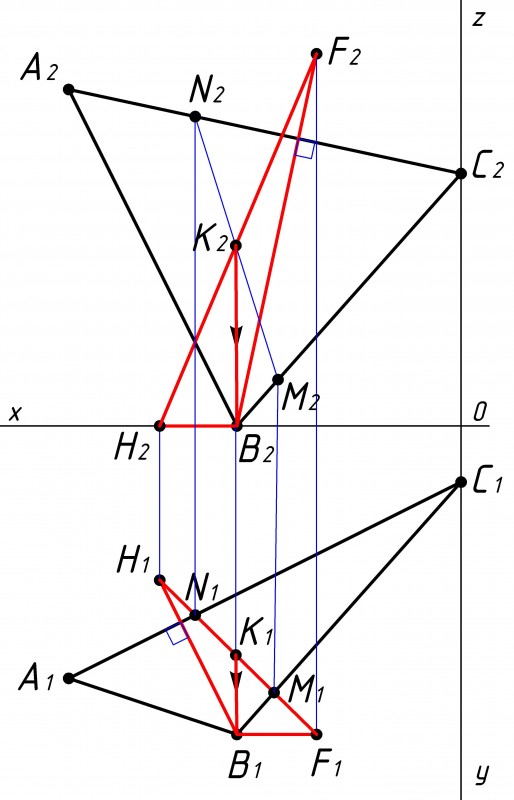
Получив вторую точку, строим линию пересечения двух треугольников (см. рис.7).

Для этого соединяем точку В с точкой К
(В₁ соединяем с К₁, В₂ соединяем с К₂).

Рис.8

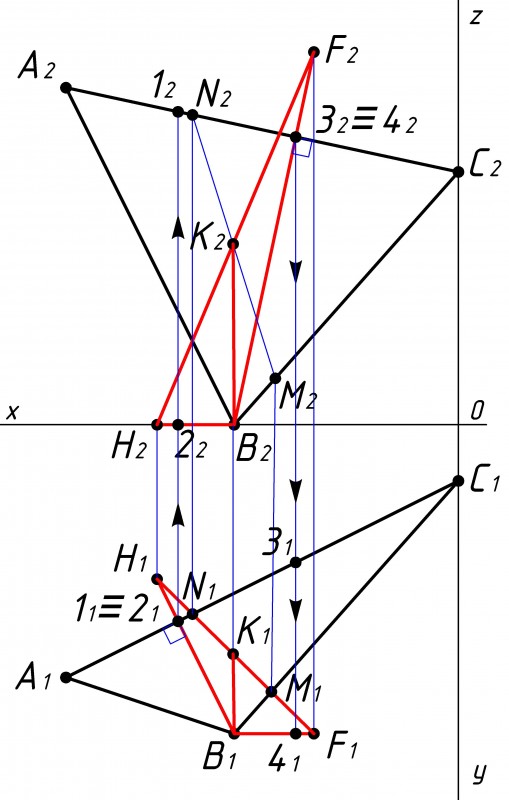
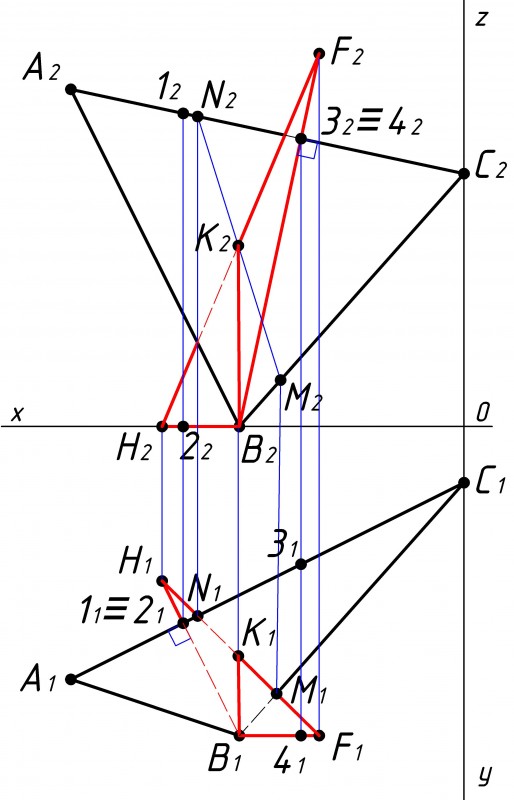
Определяем конкурирующие точки (1 и 2; 3 и 4) скрещивающихся прямых, принадлежащих плоскостям треугольников (см. рис.8).

Рассмотрим точки пересечения стороны BH и стороны АС. В точке пересечения сторон В₁Н₁ с А₁С₁ конкурируют точки 1 и 2,
а в точке пересечения сторон В₂Н₂ с А₂С₂ конкурируют точки 3 и 4.

Проецируем их на противоположную плоскость проекции, на стороны построенных треугольников, по одной точке на каждый треугольник.

Рис.9

Теперь необходимо определить видимость плоскостей с помощью полученных конкурирующих точек (1 и 2; 3 и 4) (см. рис.9).

Т.е. определяем какая плоскость перекрывает другую плоскость.
В случае с точками 1 и 2 видно, что плоскость треугольника АВС выше треугольника BFH, следовательно в точке конкурирования (1₁≡2₁) треугольник АВС будет перекрывать треугольник BFH.

В случае с точками 3 и 4, видимость определяется так. После проецирования точек видно, что точка 4₁, принадлежащая треугольнику BFH, ниже точки 3₁, принадлежащей треугольнику АВС, следовательно в точке конкурирования (3₂≡4₂) треугольник BFH будет перекрывать треугольник АВС.

Поэтому часть сторон треугольников которые перекрываются необходимо показать тонкой штриховой линией.

Рис.10

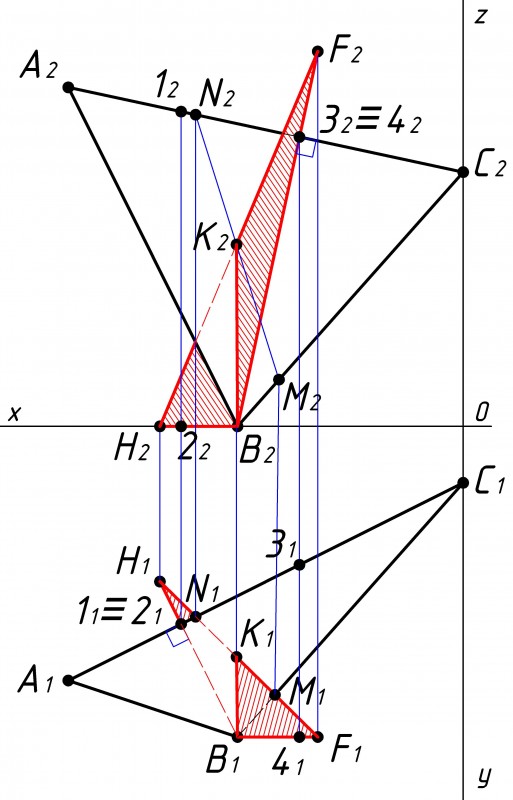
Последним шагом остается заштриховать плоскость построенного нами треугольника BFH соблюдая условие видимости (см. рис.10).