Метод прямоугольного треугольника
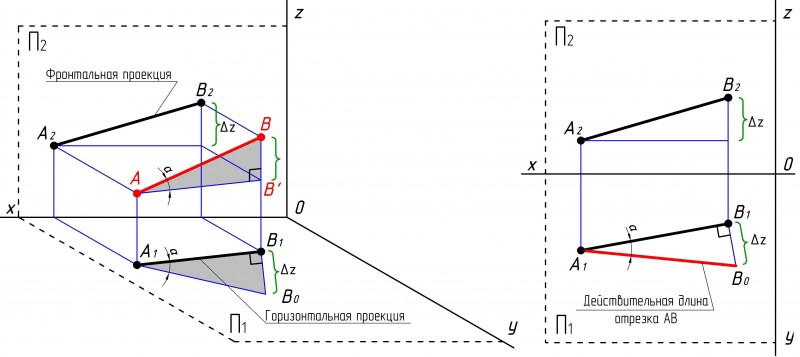
На рис.1 дается наглядное изображение проецирования прямой общего положения на плоскости проекций П1 и П2.
|
Рис.1 |
|
Через точку А провели прямую, параллельную горизонтальной проекции прямой А1В1. Получили прямоугольный треугольник АВВ' с прямым углом при вершине B', один катет которого (АВ') равен горизонтальной проекции прямой (А1В1), а другой – разности расстояний от концов А и В отрезка до горизонтальной плоскости проекций, т.е. разности координат Z (ZB - ZA = ∆Z). Таким образом, оба катета прямоугольного треугольника определяются по чертежу, следовательно, можно построить такой же треугольник А1В1В0 = АВ1В и на эпюре прямой. Одним катетом этого треугольника будет являться горизонтальная проекция отрезка А1В1, а другой катет определяют графически как разность расстояний от концов фронтальной проекции отрезка до оси ОХ. Гипотенуза А1В0 построенного треугольника равна действительной длине отрезка АВ. Угол α – это угол наклона прямой АВ к горизонтальной плоскости проекций, определяются из того же прямоугольного треугольника (угол между горизонтальной проекции отрезка и его действительной величиной). |
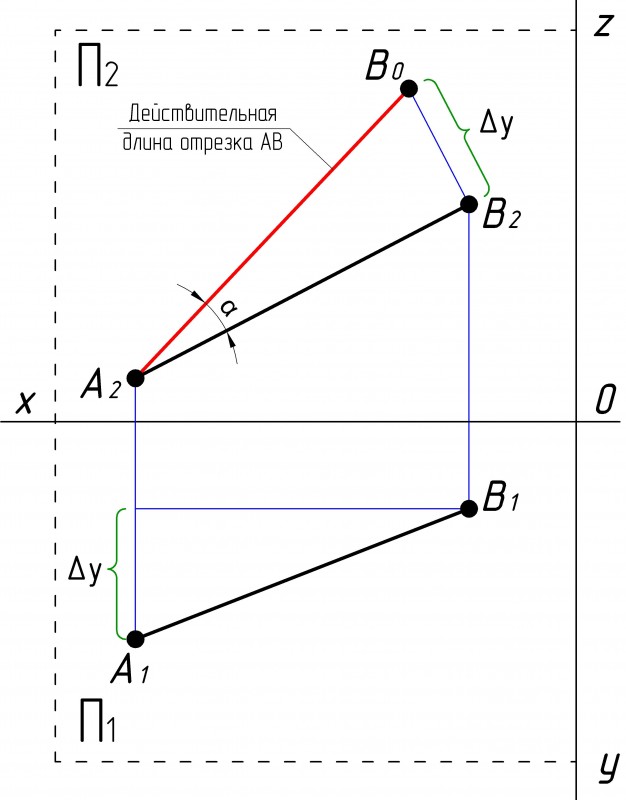
ПРИМЕР: Определить угол наклона прямой к фронтальной плоскости проекций (рис.2).
РЕШЕНИЕ: Для определения действительной длины отрезка прямой на ортогональном чертеже прямоугольный треугольник может быть построен в любой из трех плоскостей проекций. Если же необходимо определить угол его наклона к той или иной плоскости проекций, то прямоугольный треугольник следует строить в той плоскости, угол наклона к который требуется определить.
|
Рис. 2 |
Строим прямоугольный треугольник на фронтальной плоскости проекций. За один катет принимаем фронтальную проекцию (А2В2) отрезка, а за другой катет - отрезок, длина которого равна YA - YB (разности расстояний точек А и В до фронтальной плоскости проекций). Гипотенуза построенного треугольника дает нам действительную длину отрезка. Угол β между гипотенузой и фронтальной проекцией отрезка равен углу наклона прямой к фронтальной плоскости проекций. |