Построить плоскость, параллельную плоскости треугольника ABС (пример выполнения)

Рис.1

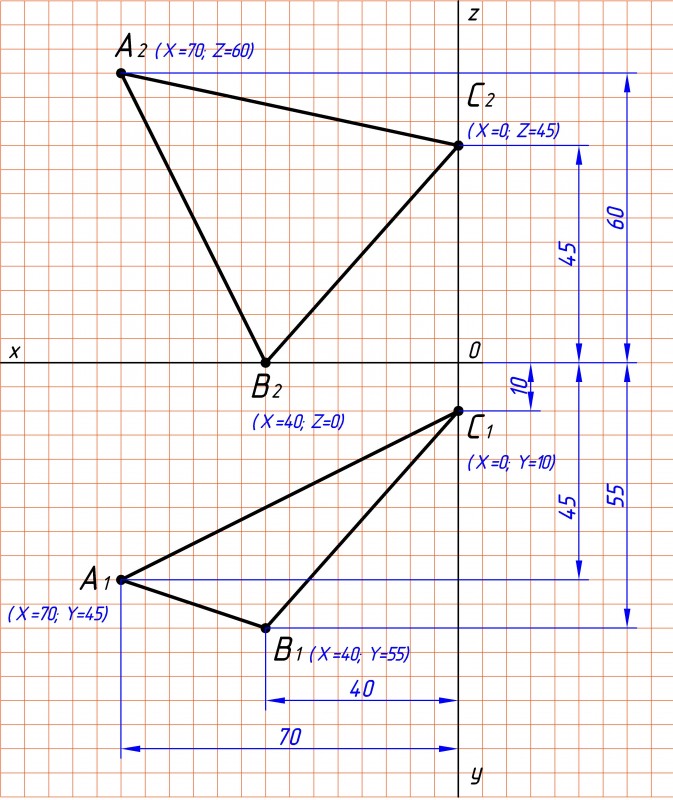
Строим плоскость треугольника АВС по заданным координатам варианта №17 (см. рис.1):

A (70, 45, 60),
B (40, 55, 0),
C (0, 10, 45).

Построить свой треугольник онлайн можно перейдя по ссылке.

Рис.2

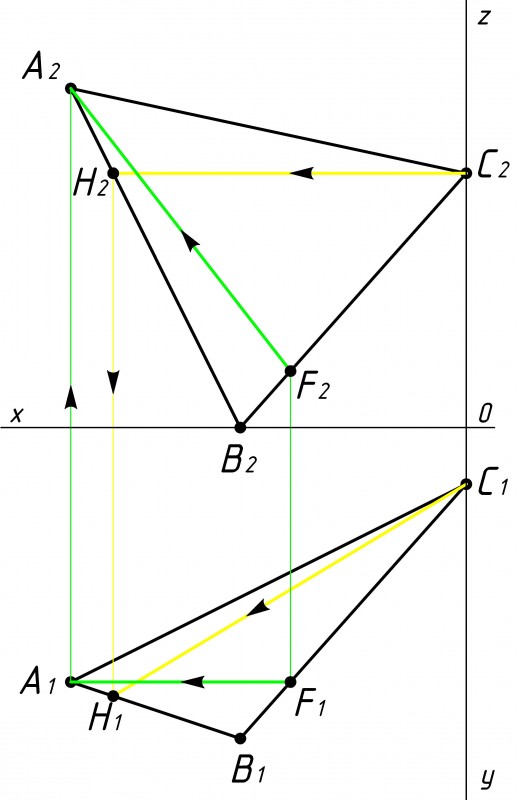
Затем строим в плоскости треугольника АВС фронталь и горизонталь (см. рис.2).

Фронталь это линия, которая параллельна оси ОХ на горизонтальной плоскости проекции (нижняя часть).
А горизонталь - линия, которая параллельна оси ОХ на фронтальной плоскости проекции (верхняя часть).
Данные линии проводятся через вершины треугольника (через точки А, B, C).

В нашем случае через вершину А мы проводим фронталь AF, а через вершину С проводим горизонталь CH.

Рис.3

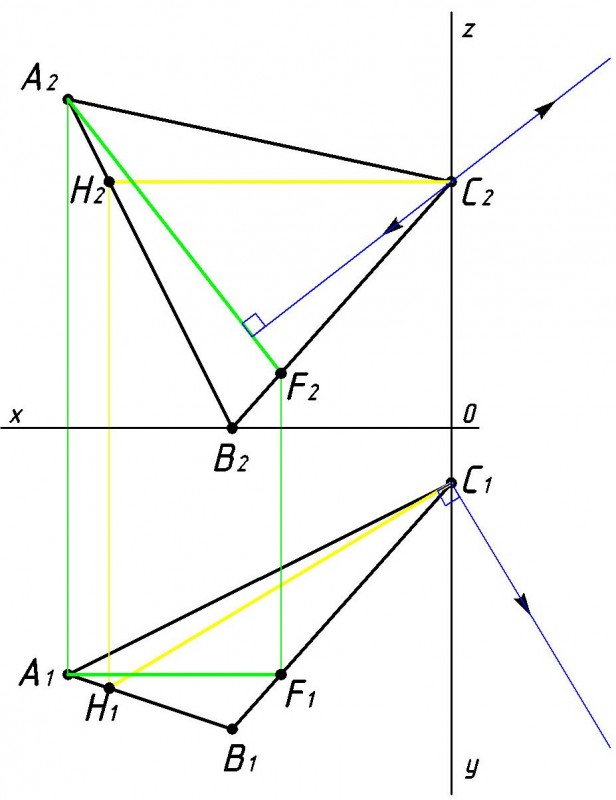
Далее необходимо через одну из вершин плоскости треугольника АВС, через которые проходят фронталь и горизонталь, или через точку их пересечения, восстановить перпендикуляр плоскости (см. рис.3).

Вершин плоскости треугольника АВС, через которые проходят фронталь и горизонталь в нашем случае являются точки А и С, точку пересечения фронтали и горизонтали рассматривать не будем.

Берем одну из этих точек, например точку С, и из нее восстановим перпендикуляр плоскости. При этом горизонтальную проекцию перпендикуляра проводим перпендикулярно к горизонтальной проекции горизонтали C₁H₁, а фронтальную проекцию перпендикулярно к фронтальной проекции фронтали C₂H₂.

Рис.4

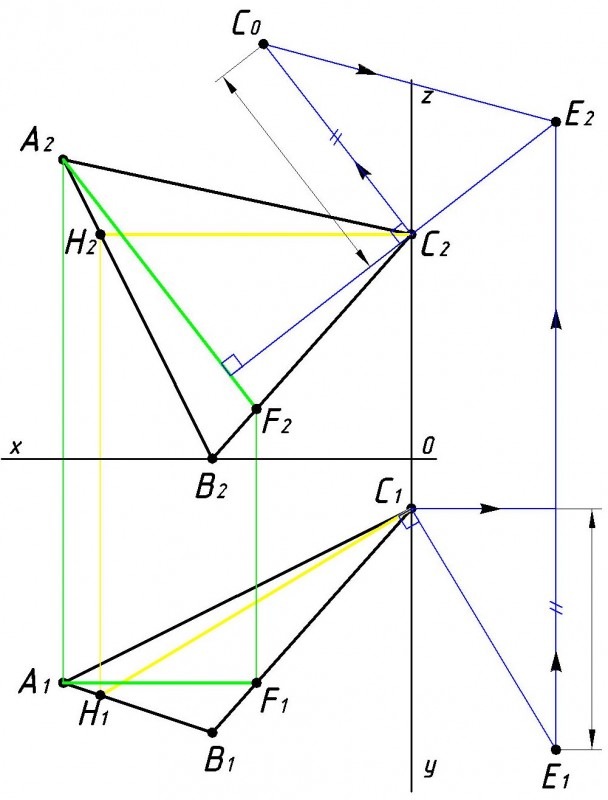
Теперь нужно определить действительную длину данного перпендикуляра,  методом прямоугольного треугольника (см. рис.4).

Берем на нашем перпендикуляре произвольную точку Е и определяем способом прямоугольного треугольника действительную длину полученного отрезка перпендикуляра. Определяем расстояние по вертикали от точки E до точки C на какой-либо плоскости проекций.

Например на горизонтальной (нижней) плоскости проекции. Откладываем это расстояние перпендикулярно отрезку C₂E₂ на противоположной плоскости проекции (в нашем случа на фронтальной) от любой из вершин (например от точки C₂) и получили нулевую точку C₀.

Расстояние от точки C₀ до точки E₂ и является действительной длиной проведенного нами перпендикуляра CE.

Рис.5

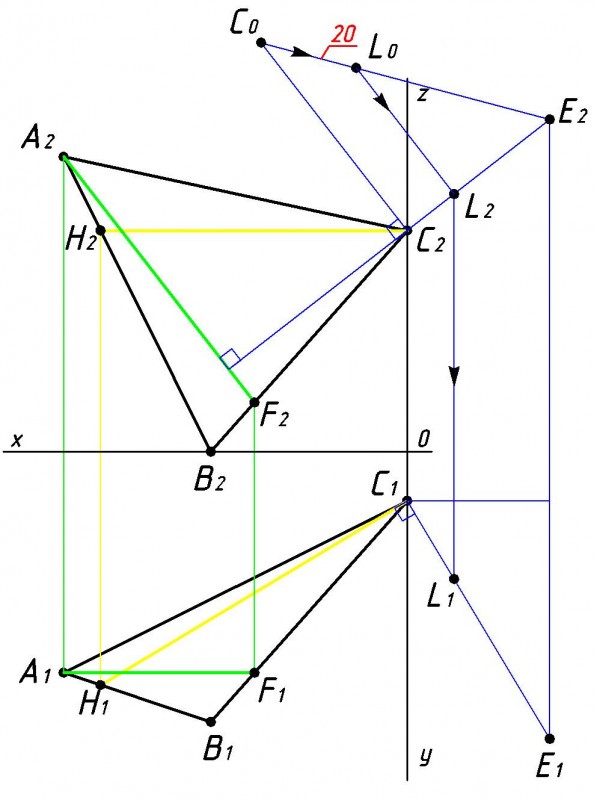
Далее нужно на полученной действительной величине перпендикуляра отложить нужное нам расстояние, на которое должна отстоять паральлельная плоскость от плоскости треугольника АВС (см. рис.5).

На натуральной величине построенного отрезка перпендикуляра находим точку L₀, расположенную на заданном расстоянии (например 20 мм) от плоскости треугольника, от точки вершины, (в нашем случае точки C).

После того как мы получили точку L₀, необходимо построить проекции этой точки (L₂ и L₁ на проекциях перпендикуляра.

Рис.6

Последним шагом будет построение проекций искомой плоскости (см. рис.6)

После того как мы построили точки L₁ и L₂, необходимо провести через них проекции искомой плоскости, задаем ее двумя пересекающимися прямыми, соблюдая условие параллельности плоскостей.

Условие: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Следовательно нужную нам плоскость задаем двумя прямыми, параллельными сторонам треугольника АВС (в нашем случае сторонам ВС и АС).