Определить расстояние от точки D до плоскости треугольника АВС (пример выполнения)

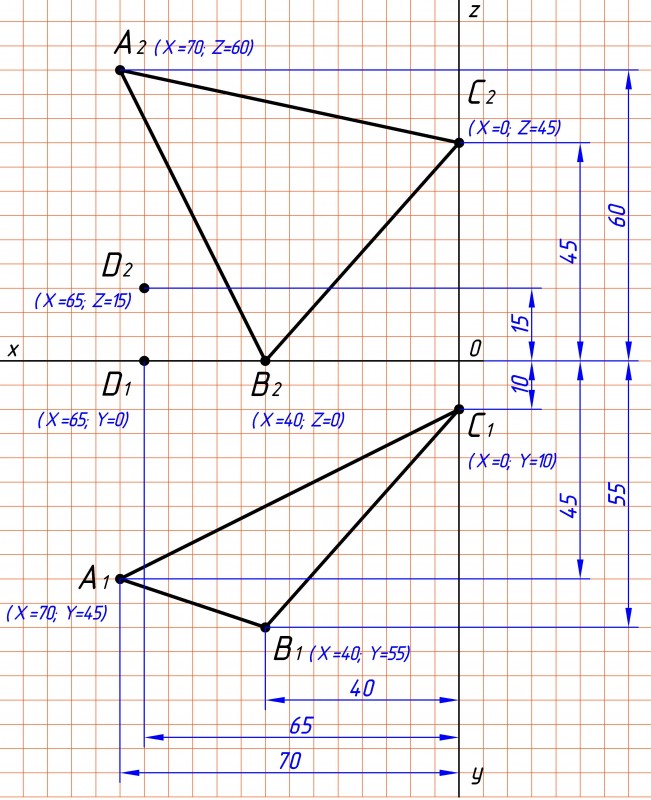
Рис.1

Строим плоскость треугольника АВС и точку D по заданным координатам варианта №17 (см. рис.1):

A (70, 45, 60),
B (40, 55, 0),
C (0, 10, 45),
D (65, 0, 15).

Построить свой треугольник онлайн можно перейдя по ссылке.

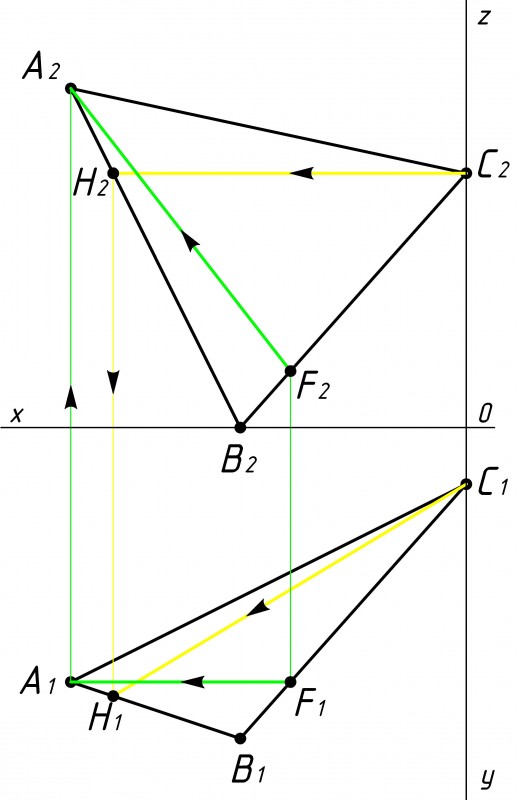
Рис.2

Затем строим в плоскости треугольника АВС фронталь и горизонталь (см. рис.2).

Фронталь это линия, которая параллельна оси ОХ на горизонтальной плоскости проекции (нижняя часть).
А горизонталь - линия, которая параллельна оси ОХ на фронтальной плоскости проекции (верхняя часть).

Данные линии проводятся через вершины треугольника (через точки А, B, C). В нашем случае через вершину А мы проводим фронталь AF, а через вершину С проводим горизонталь CH.

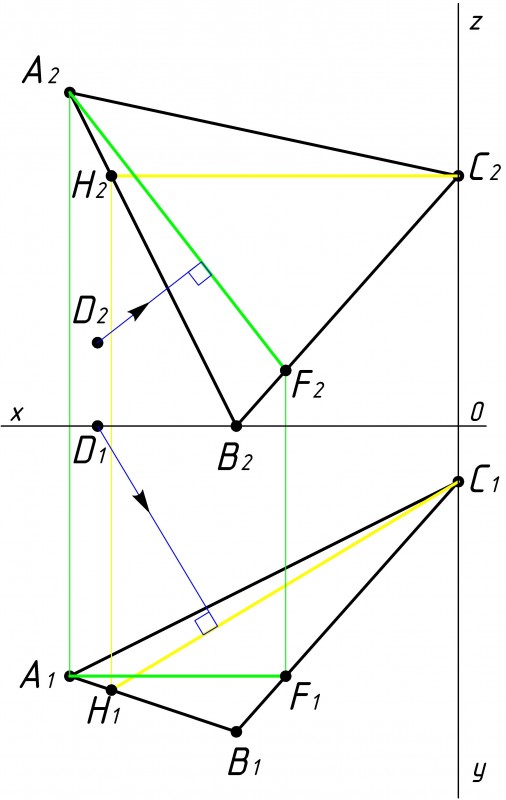
Рис.3

После того как мы построили фронталь и горизонталь, необходимо из точки D провести перпендикуляр к треугольнику АВС(см. рис.3).

При этом горизонтальная проекция перпендикуляра (от точки D₁) должна быть перпендикулярна к горизонтальной проекции горизонтали C₁H₁.

А фронтальная проекция (от точки D₂) перпендикулярна к фронтальной проекции фронтали A₂F₂;

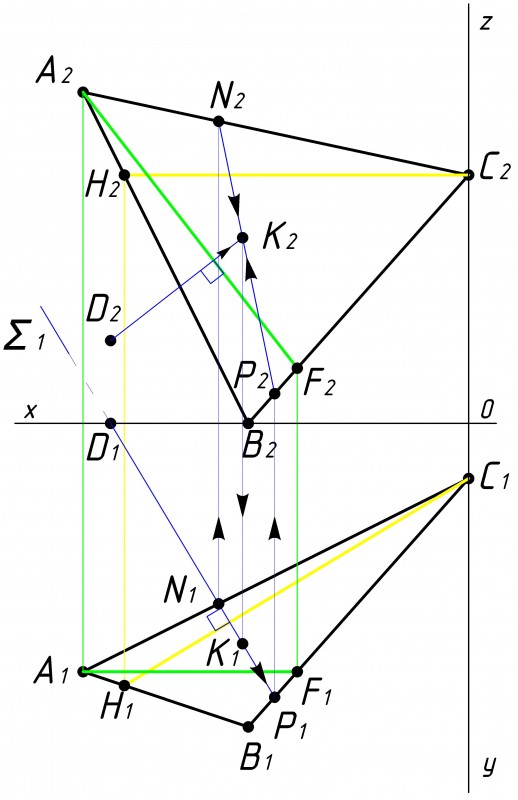
Рис.4

Теперь необходимо определить точку пересечения перпендикуляра с данной плоскостью, заключив перпендикуляр во вспомогательную плоскость частного положения (см. рис.4).

Перпендикуляр через точку D₁ заключаем во вспомогательную плоскость частного положения ∑₁

Примечание: необязательно это делать через точку D₁, результат через точку D₂ будет идентичным.

Так же необязательно рисовать вспомогательную плоскость частного положения ∑₁, ее можно просто представить, что мы ее там проводим.

После того как мы провели вспомогательную плоскость ∑₁ находим точки пересечения данной плоскости (M₁P₁) с треугольником АВС. Проецируем их на фронтальную плоскость проекции и получаем точки M₂P₂.

Потом находим точку пересечения линии M₂P₂ вспомогательной плоскости с перпендикуляром от точки D₂ и отмечаем точку К₂. Проецируем точку К₂ на горизонтальной плоскости проекции и получаем точку К₁.

Рис.5

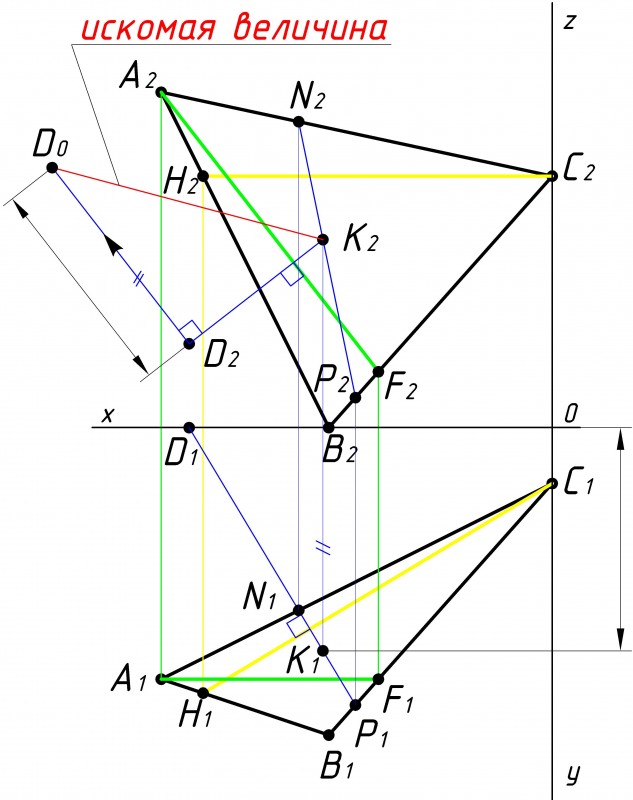
После того как мы провели перпендикуляр DK, осталось определить его действительную величину  способом прямоугольного треугольника (см. рис.5).

Определяем расстояние по вертикали от точки D до точки K на какой-либо плоскости проекций. Например на горизонтальной (нижней) плоскости проекции.

Откладываем это расстояние перпендикулярно отрезку DK на противоположной плоскости проекции (в нашем случа на фронтальной) от любой из вершин (например от точки D) и получили нулевую точку D₀.

Расстояние от точки D₀ до точки K₂ и является искомым расстоянием от точки D до плоскости треугольника АВС.

Рис.6

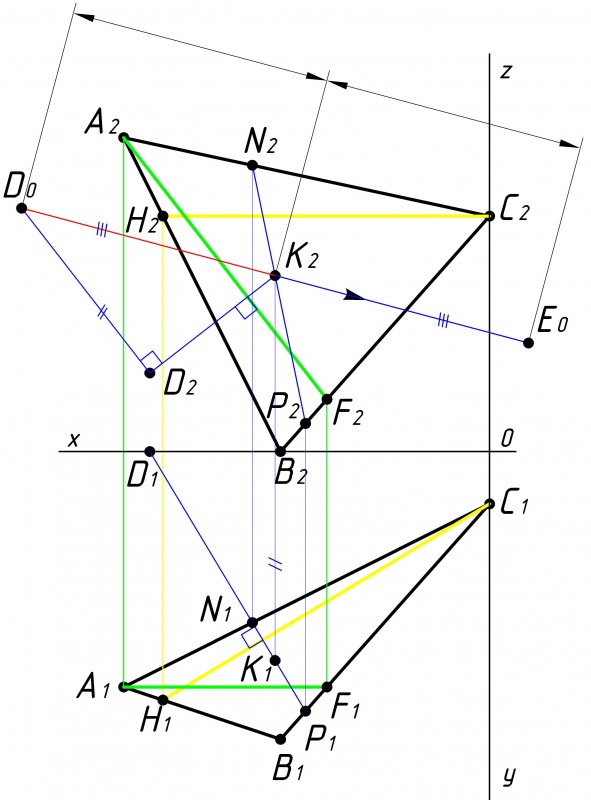
Найдя расстояние от точки до плоскости треугольника АВС, можно начать строить точку симметричную точке D относительно данного треугольника (см. рис.6).

Симметричная точка подразумевает собой точку, которая отстоит от плоскости треугольника АВС на таком же расстоянии, что и точка D, но с противоположной стороны.

Рассмотрим полученный нами отрезок D₀K₂. В противоположную сторону от точки K₂ откладываем отрезок равный D₀K₂. Ставим точку Е₀.

Рис.7

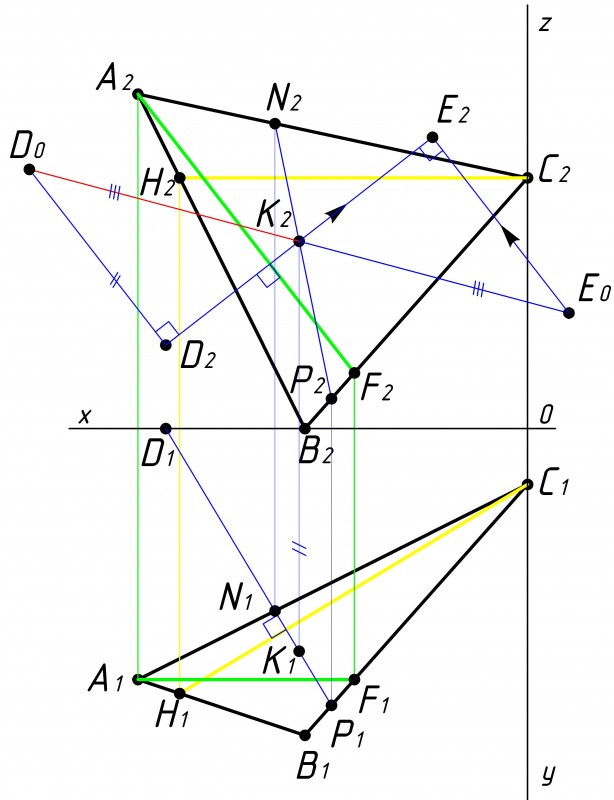
Затем проводим перпендикуляр к линии пенпендикуляра от точки D на рассматриваемой плоскости проекции (см. рис.7).

В нашем случае на фронтальной плоскости проекции к удлиненной линии D₂K₂. На пересечении ставим точку Е₂.
Линии D₂K₂ и К₂Е₂ так же равны между собой.

Рис.8

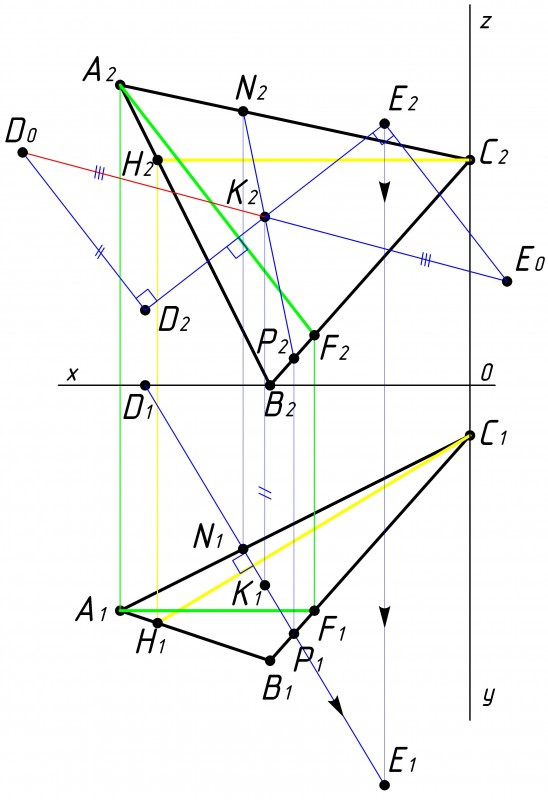
Строим проекцию полученной точки на противоположную плоскость проекции так же на линию перепендикуляра (см. рис.8).

В нашем случае проецируем полученную точку Е₂ на горизонтальную плоскость проекции на линию перепендикуляра (удлинненную линию D₁K₁). Получаем точку Е₁. Линии D₁K₁ и К₁Е₁ так же равны между собой.